Enumerate balanced ideals
A program to enumerate balanced ideals in Weyl groups. These are subsets of the Weyl group W which are ideals with respect to the Bruhat order and which are mapped to their complement by the involution on W which is given by left-multiplication with the longest element.
Balanced ideals were used by Kapovich-Leeb-Porti to construct cocompact domains of discontinuity in flag manifolds for the action of Anosov representations. Essentially, their result says that, if P and Q are two parabolic subgroups of a Lie group G and W its restricted Weyl group, then for every P-Anosov representation and every balanced ideal in W which is left-invariant by P∩W and right-invariant by Q∩W, there is one cocompact domain of discontinuity in the flag manifold G/Q.
As the number of balanced ideals grows superexponentially with the rank of the Lie group, we have made some effort to optimize the enumeration algorithm. For example, the ideals are stored as bit vectors, so that set operations can be realized as bitwise operations. Also, only half of the ideal is stored, as the other half can be reconstructed from the balanced condition. With these and some other tricks we get an algorithm which can find tens of millions of balanced ideals per second on a single core (although outputting them is a lot slower, so this is mostly useful for determining the number of balanced ideals).
Setup
You need a terminal, gcc, and GNU Make. Navigate to the folder and run make. This produces the executables enumerate and graph. Their usage is described below.
Usage
In the most basic case, we just specify a Weyl / Coxeter group by giving its Cartan type as the first argument, for example C3, G2, A1A2 (for the direct product of A1 and A2) etc. The output will be a list of all balanced ideals. For example:
$ ./enumerate A3
A3
Rank: 3 Order: 24 Positive Roots: 6 Cosets: 24
Balanced ideals:
0 left: a c right: ab gen: caba
1 left: a c right: bc gen: abcb
2 left: right: gen: cba acb abc
3 left: right: gen: cba acb aba bc
4 left: right: gen: cba abc bac
5 left: right: a gen: cba aba bac
6 left: right: gen: acb abc bcb ba
7 left: right: b gen: acb aba bcb
8 left: right: c gen: abc bac bcb
9 left: b right: gen: aba bac bcb
Found 10 balanced ideals
There is one line for each balanced ideal. The first column is an index, the next two columns show the left- and right-invariance of the ideal as a subset of the generators a,b,c of the Weyl group (see below for an explanation of the labeling). Finally a minimal generating set of the balanced ideal is shown, in the sense that it is the smallest ideal containing these Weyl group elements.
If we are only interested in balanced ideal with a certain left- and right-invariance, we cangive these as the second and third arguments. The subsets will be divided out in the beginning and the enumeration algorithm will run on the double cosets, making this also a lot faster.. The empty set can be specified as "-", so enumerate A4 - - does the same as enumerate A4.
$ ./enumerate C5 a bcde
<a> \ C5 / <bcde>
Rank: 5 Order: 3840 Positive Roots: 25 Cosets: 16
Balanced ideals:
0 left: abcd right: bcde gen: bcdabcaba
1 left: ab de right: bcde gen: edbcaba
2 left: a cd right: bcde gen: cdbcaba edcba
Found 3 balanced ideals
Finally, we can control the amount of output using the environment variable OUTPUT_LEVEL. Values from 0 to 4 are valid. The default is 2. For example:
OUTPUT_LEVEL=0means no output at all. This is rarely useful.OUTPUT_LEVEL=1only shows the number of balanced ideals (in addition to some basic info about the group). This is currently the only mode that can take full advantage of the speed of the enumeration algorithm.OUTPUT_LEVEL=2(the default) additionally prints one line for every balanced ideal found, as explained above.OUTPUT_LEVEL=3additionally shows the list of all double cosets, giving a minimal wordlength representative for each of them.OUTPUT_LEVEL=4prints the same, and also the Bruhat order on the double cosets as a dot file (which can be rendered by Graphviz), and the involution on the double quotient. If you only want to see the Bruhat order, it is better to use thegraphtool, which is made specifically for that.
$ OUTPUT_LEVEL=1 ./enumerate C4
C4
Rank: 4 Order: 384 Positive Roots: 16 Cosets: 384
Found 49404510 balanced ideals
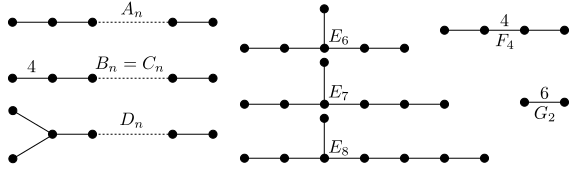
Labeling of the Weyl group generators
The allowed Cartan types are An, Bn, Cn, Dn, E6, E7, E8, F4 and G2, where n is any positive integer, plus any direct products of them. The Coxeter group generators / simple roots are labeled a,b,c,d,..., first by direct factor, and then from left to right in the following diagram. So for example in the Cartan type C2C3, the generators are a,b,c,d,e, with the products ab and cd having order 4, de having order 3 and any other pair commuting.