Enumerate balanced ideals

This program, which I made together with David Dumas, enumerates all balanced ideals in a Weyl group, or all balanced ideals with a specified left- and right-invariance. These can be used to construct cocompact domains of discontinuity for Anosov representations, as explained by Kapovich, Leeb and Porti in arXiv:1306.3837.

You can download it here. To compile you just need a gcc and GNU make. If you have questions, just email me at w18@florianstecker.de.

How to use it

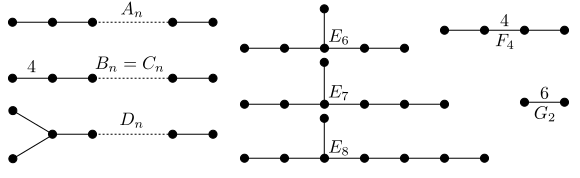
Specify a Weyl group / Coxeter group as the first argument(s), for example C3, G2, A1 A2, etc. and it will output a list of all balanced ideals. For every ideal the left- and right-invariance is shown as well as a list of generating elements. The Coxeter group generators / simple roots are labeled a,b,c,d,..., essentially from left to right in this diagram:

An example:

$ ./enumerate A3
A3
Rank: 3 Order: 24       Positive Roots: 6       Cosets: 24

Balanced ideals:
   0 left: a c right: ab  gen: caba
   1 left: a c right:  bc gen: abcb
   2 left:     right:     gen: cba acb abc
   3 left:     right:     gen: cba acb aba bc
   4 left:     right:     gen: cba abc bac
   5 left:     right: a   gen: cba aba bac
   6 left:     right:     gen: acb abc bcb ba
   7 left:     right:  b  gen: acb aba bcb
   8 left:     right:   c gen: abc bac bcb
   9 left:  b  right:     gen: aba bac bcb

Found 10 balanced ideals

We can also specify two subsets of the simple roots as second and third argument. Then only balanced ideals with these invariances will be enumerated (the subsets will be divided out in the beginning, making this also a lot faster). The empty set can be specified as "-".

$ ./enumerate C5 a bcde
<a> \ C5 / <bcde>
Rank: 5 Order: 3840     Positive Roots: 25      Cosets: 16

Balanced ideals:
   0 left: abcd  right:  bcde gen: bcdabcaba
   1 left: ab de right:  bcde gen: edbcaba
   2 left: a cd  right:  bcde gen: cdbcaba edcba

Found 3 balanced ideals

Finally, we can control the amount of output using the environment variable OUTPUT_LEVEL. Values from 0 to 4 are valid. The default is 2. For example:

$ OUTPUT_LEVEL=1 ./enumerate C4
C4
Rank: 4 Order: 384      Positive Roots: 16      Cosets: 384

Found 49404510 balanced ideals