florian/coxeter_automaton
1
0
Fork 0
Code Issues Pull Requests Projects Releases Wiki Activity

center images in doc

Browse Source
This commit is contained in:
Florian Stecker 2023-01-04 23:36:46 +01:00
parent 3d81dc667d
commit aadfd61c43
1 changed files with 3 additions and 3 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

6
README.md
View File

@ -8,7 +8,7 @@ The construction of the first automaton is explained in detail in the book by [B
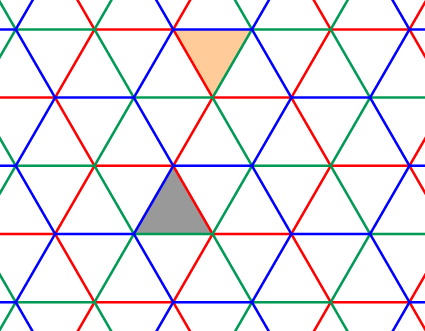
To explain what these automata are about, let's have a look at the tiling of the Euclidean plane by equilateral triangles, as drawn below. To explain what these automata are about, let's have a look at the tiling of the Euclidean plane by equilateral triangles, as drawn below.
![Euclidean tiling](https://florianstecker.net/git_files/coxeter_automaton/tiling.png) ![Euclidean tiling](https://florianstecker.net/git_files/coxeter_automaton/tiling.png){: .center}
Any triangle in the tiling can be obtained from the gray one by successively reflecting it along some of its sides. For example, to get to the orange triangle we could use the sequences of reflections Any triangle in the tiling can be obtained from the gray one by successively reflecting it along some of its sides. For example, to get to the orange triangle we could use the sequences of reflections
@ -18,11 +18,11 @@ Any triangle in the tiling can be obtained from the gray one by successively ref
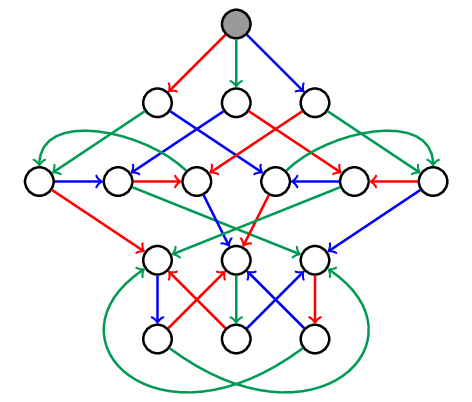
The first two sequences are _reduced_, which means they have the minimal number of reflections (5) necessary to reach their endpoint, the orange triangle. In other words, in a reduced sequence every step gets us further away from the starting triangle. The set of all reduced sequences is described by the following automaton. Every path starting from the gray vertex corresponds to a reduced sequence, and vice-versa. The first two sequences are _reduced_, which means they have the minimal number of reflections (5) necessary to reach their endpoint, the orange triangle. In other words, in a reduced sequence every step gets us further away from the starting triangle. The set of all reduced sequences is described by the following automaton. Every path starting from the gray vertex corresponds to a reduced sequence, and vice-versa.
![Automaton generating all reduced words](https://florianstecker.net/git_files/coxeter_automaton/geodesic_automaton.png) ![Automaton generating all reduced words](https://florianstecker.net/git_files/coxeter_automaton/geodesic_automaton.png){: .center}
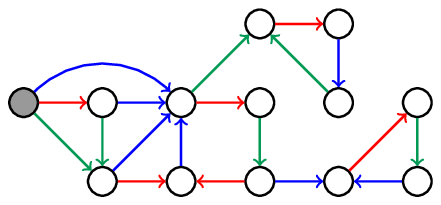
In the above, multiple sequences might lead to the same triangle. To get unique labels, we can instead restrict ourselves to only the lexicographically minimal sequence for every triangle. For the orange triangle above, and with the order `red < green < blue`, that would be the sequence `red-blue-red-green-red`. The following automaton yields all lexicographically minimal reduced words. In the above, multiple sequences might lead to the same triangle. To get unique labels, we can instead restrict ourselves to only the lexicographically minimal sequence for every triangle. For the orange triangle above, and with the order `red < green < blue`, that would be the sequence `red-blue-red-green-red`. The following automaton yields all lexicographically minimal reduced words.
![Automaton generating all lex reduced words](https://florianstecker.net/git_files/coxeter_automaton/lex_automaton.png) ![Automaton generating all lex reduced words](https://florianstecker.net/git_files/coxeter_automaton/lex_automaton.png){: .center}
What this program can do is produce these two automata, not only for the equilateral triangle tiling, but for any [Coxeter group]. Essentially, Coxeter groups correspond to all tilings generated by reflections along the sides of a convex polyhedron in projective space, in arbitrary dimensions. This includes regular triangulations of Euclidean and hyperbolic space. What this program can do is produce these two automata, not only for the equilateral triangle tiling, but for any [Coxeter group]. Essentially, Coxeter groups correspond to all tilings generated by reflections along the sides of a convex polyhedron in projective space, in arbitrary dimensions. This includes regular triangulations of Euclidean and hyperbolic space.