coxeter_automaton.py - Find geodesic automata for Coxeter groups
This Python code computes two kinds of finite automata for any Coxeter group: one which consumes every reduced word, and one which consumes only the lexicographically minimal reduced word for each group element. These automata are then used to enumerate all group elements up to a given word length.
The construction of the first automaton is explained in detail in the book by Björner-Brenti. The key results leading to the second automaton are from Brink-Howlett.
Simple example
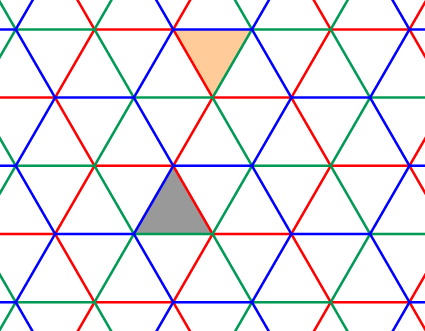
To explain what these automata are about, let's have a look at the tiling of the Euclidean plane by equilateral triangles, as drawn below.
Any triangle in the tiling can be obtained from the gray one by successively reflecting it along some of its sides. For example, to get to the orange triangle we could use the sequences of reflections
red-blue-red-green-red
blue-red-blue-green-red
blue-red-green-blue-green-blue-red
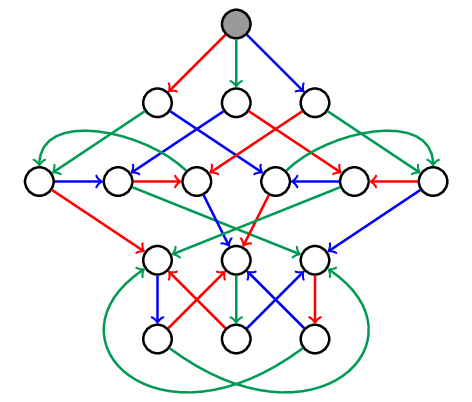
The first two sequences are reduced, which means they have the minimal number of reflections (5) necessary to reach their endpoint, the orange triangle. In other words, in a reduced sequence every step gets us further away from the starting triangle. The set of all reduced sequences is described by the following automaton. Every path starting from the gray vertex corresponds to a reduced sequence, and vice-versa.
In the above, multiple sequences might lead to the same triangle. To get unique labels, we can instead restrict ourselves to only the lexicographically minimal sequence for every triangle. For the orange triangle above, and with the order red < green < blue, that would be the sequence red-blue-red-green-red. The following automaton yields all lexicographically minimal reduced words.
What this program can do is produce these two automata, not only for the equilateral triangle tiling, but for any Coxeter group. Essentially, Coxeter groups correspond to all tilings generated by reflections along the sides of a convex polyhedron in projective space, in arbitrary dimensions. This includes regular triangulations of Euclidean and hyperbolic space.
Usage
See example.py. The function generate_automaton_coxeter_matrix takes as argument the Coxeter matrix of the desired group and a boolean determining which of the two automata is generated. It returns the automaton as an adjacency list. In addition, the function enumerate_group can compute all group elements up to a given word length, including the edges of the Cayley graph. To do this, it uses both automata.
For example, the following code would give us the first of the two automata above:
#!/usr/bin/python
import coxeter_automaton
coxeter_matrix = [[1, 3, 3],
[3, 1, 3],
[3, 3, 1]]
graph = coxeter_automaton.generate_automaton_coxeter_matrix(coxeter_matrix, lex_reduced = False)
print(graph)
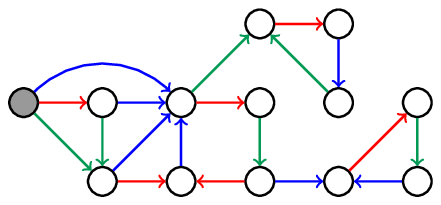
For a more human-readable output, dot_graph.py generates dot files, which can be used as input to Graphviz to render the graph as a PDF file. The resulting images are not quite as nice as the manually drawn ones above, but usually good enough to be useful.