| About | Research | Teaching | Programs | Pictures | Other |
My current research interests revolve around discrete subgroups of semisimple Lie groups, and in particular Anosov representations. Below are some projects I have worked on or am working on.
León Carvajales and Florian Stecker, arXiv:2308.08607
We study the action of an Anosov subgroup of a semisimple Lie group G on a homogeneous space X = G/H, where H is a closed subgroup of G. As the only condition, we require that the diagonal action of G on the product of its flag manifold with X has only finitely many orbits. This is true if X is a flag manifold (a well-studied case, see my other papers below for example), but also if X is a (pseudo-Riemannian) symmetric space or more generally a “spherical homogeneous space”. Then we can construct domains of discontinuity in X, open subsets on which the Anosov subgroup acts properly. Our construction generalizes the one for flag manifolds. We analyse the case that X is a symmetric space in more detail, and find a refinement of our construction which sometimes yields larger domains. Under some conditions, we even manage to prove that these domains are the largest possible ones.
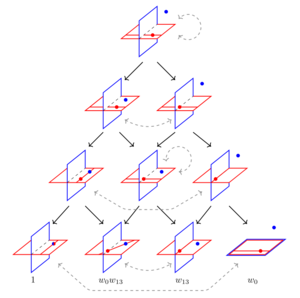
Gye-Seon Lee, Jaejeong Lee and Florian Stecker, arXiv:2106.11349
We wanted to understand what the set of Anosov representations in the character variety looks like, by looking at the simplest example where it’s not just a union of connected components. The SL(3,R) character variety of a hyperbolic triangle reflection group is 1-dimensional, so that’s a good candidate. It has a lot of connected components, each homeomorphic to the real line, but we ended up showing that only two of them contain Anosov representations: the “Hitchin component”, in which every representation is Anosov, and the “Barbot component”, in which a representation is Anosov if and only if a certain group element (the “Coxeter element”) has distinct real eigenvalues. That means, the Barbot component contains a closed interval of non-Anosov representations, and everything outside of it is Anosov.
Florian Stecker, arXiv:1810.11496 (published in Geometriae Dedicata)
I examined a construction by Kapovich-Leeb-Porti of cocompact domains of discontinuity for Anosov representations in flag manifolds. In this paper, I show a “converse” in the case of Borel Anosov representations: up to some exceptions in small ranks, every domain of discontinuity must be contained in, and every cocompact one must be equal to, one of the KLP examples. In particular, this shows there are only finitely many cocompact domains of discontinuity. For example, the table on the left shows their number in the Grassmannian Gr(k,n) for an SL(n,R) Hitchin representation.
Florian Stecker and Nicolaus Treib, arXiv:1806.04459 (published in J. London Math. Soc.)
This project also starts out with Kapovich-Leeb-Porti’s construction of cocompact domains of discontinuity for Anosov representations in flag manifolds. We noticed that this construction can be extended to “oriented flag manifolds”, which are finite covers of the ordinary flag manifold. Somewhat surprisingly, this gives a lot more freedom to find such domains. We give a bunch of examples which are genuinely new in this oriented situation. The simplest one is shown on the left: certain free groups in SL(3,R) act on the 2-sphere with a Cantor set of “half great circles” removed, in a way that the quotient is a compact manifold.
My PhD thesis has a lot of overlap with my papers, but also has a few additional bits and gives some context.
My Master’s thesis on the moduli space of solutions to Hitchin’s equations (closely related to the moduli space of Higgs bundles). I showed in detail how to construct this moduli space as a Hyperkähler quotient of infinite dimensional (Hilbert) manifolds. This includes a slice theorem for Hilbert manifolds, and dealing with some analytical details around Sobolev spaces and regularity theory.
My Bachelor’s thesis in physics was on cosmological simulations in astrophysics. These are simulations of how the universe evolved from miniscule density fluctuations shortly after the big bang up to the current state. In my thesis, I tried to find voids, large empty spaces between galaxy clusters, in the output of these simulations. Algorithms to do this existed, but I had to modify them to work on our massive simulations containing over a billion matter particles.